Chương 4: Tiên Đoán Tương Lai
S
ự biến mất của thông tin trong các hố đen có thể làm giảm khả năng tiên đoán tương lai của chúng ta như thế nào.

Nhân loại luôn mong muốn điều khiển tương lai, hoặc ít nhất là đoán trước được điều gì sẽ xảy ra. Đó là lý do tại sao ngành chiêm tinh học lại phổ biến đến thế. Chiêm tinh học cho rằng các sự kiện xảy ra trên trái đất đều liên quan đến chuyển động của các hành tinh trên bầu trời. Đây là một giả thiết có thể kiểm chứng một cách khoa học, à không, nó sẽ là một giả thiết có thế kiểm chứng một cách khoa học nếu như các nhà chiêm tinh dám mạo hiểm nói một dự đoán chắc chắn mà có thể kiểm tra được. Tuy nhiên, họ cũng đủ thông minh để chỉ nói những dự đoán mơ hồ có thể đúng với bất kỳ kết quả nào. Những phát biểu kiểu như “Các mối quan hệ cá nhân có thể trở lên mãnh liệt hơn” hoặc là “Bạn sẽ có một cơ may về tài chính” sẽ không bao giờ bị chứng minh là sai cả.

“Tháng này sao Hỏa chiếm cung Nhân mã, đó là thời gian tốt để bạn tự học. Sao Hỏa yêu cầu bạn sống một cuộc sống theo cách bạn cho là đúng và thường những người khác cho là sai. Và những điều đó sẽ xảy ra.
Vào ngày 20, sao Hỏa sẽ đi đến phần học vấn của bạn, nó liên quan đến nghề nghiệp và bạn sẽ học để nhận lấy trách nhiệm và giải quyết các quan hệ khó khăn.
Tuy vậy, đến kỳ trăng rằm bạn sẽ có được một sự thông suốt và tầm bao quát tuyệt vời về toàn bộ cuộc đời mà bạn sẽ nhận được.”
Nhưng lý do mà phần đông các nhà khoa học không tin vào chiêm tinh học không phải là những bằng chứng phi khoa học hoặc thiếu những bằng chứng khoa học mà vì nó không phù hợp với những lý thuyết khác đã được kiểm chứng bằng thực nghiệm. Khi Copernicus và Galileo phát hiện ra rằng các hành tinh quay quanh mặt trời chứ không phải quay quanh trái đất, và Newton tìm ra định luật hấp dẫn điều khiển chuyển động của các hành tinh thì chiêm tinh học trở lên cực kỳ đáng ngờ. Tại sao vị trí của các hành tinh khác trên nền trời khi chúng được nhìn từ trái đất lại có những mối tương quan với những đại phân tử tự gọi là sinh vật có trí tuệ sống trên một tiểu hành tinh? (hình 4.1) Chiêm tinh học còn phải làm cho chúng ta tin vào sự tương quan đó. Các lý thuyết được trình bày trong cuốn sách này cũng không hơn gì chiêm tinh học ở chỗ không có thêm các bằng chứng thực nghiệm để củng cố các lý thuyết đó, nhưng ta vẫn tin vì các lý thuyết này phù hợp với các lý thuyết đã được kiểm chứng.
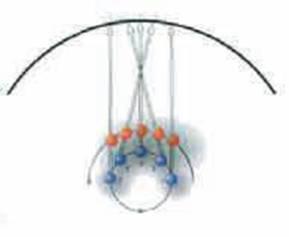
(Hình 4.1)
Một người quan sát trên trái đất (màu xanh) đang chuyển động trên quĩ đạo xung quanh mặt trời sẽ thấy sao Hỏa (màu đỏ) in trên vòng cầu các sao.
Chuyển động biểu kiến phức tạp của các hành tinh có thể được giải thích bằng các định luật của Newton và không có ảnh hưởng gì đến số phận của con người.
Sự thành công của các định luật của Newton và các lý thuyết vật lý khác dẫn đến ý tưởng về quyết định luận khoa học (scientific determinism). Ý tưởng này được một nhà khoa học người Pháp tên là Marquis de Laplace đưa ra lần đầu tiên vào đầu thế kỷ thứ mười chín. Laplace cho rằng nếu chúng ta biết được vị trí và tọa độ của tất cả các hạt trong vũ trụ tại một thời điểm thì các định luật vật lý sẽ cho phép chúng ta đoán được trạng thái của vũ trụ sẽ như thế nào tại bất kỳ một thời điểm nào khác trong quá khứ và tương lai (hình 4.2).
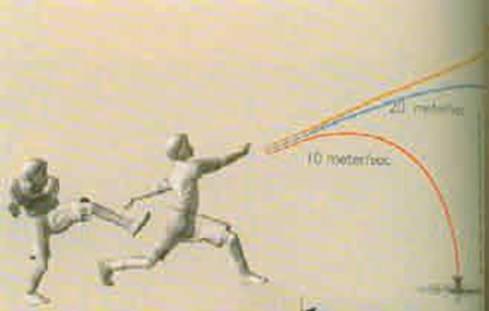

(Hình 4.2)
Nếu bạn biết vị trí và tốc độ của quả bóng mà bạn ném đi, bạn có thể tính được nó sẽ đi đến đâu.
Nói cách khác, nếu quyết định luận khoa học mà đúng thì chúng ta có thể đoán trước được tương lai và không cần đến chiêm tinh học. Tất nhiên là trên thực tế ngay cả những cái đơn giản như định luật hấp dẫn của Newton cũng dẫn đến các phương trình mà chúng ta không thể giải một cách chính xác cho hệ có nhiều hơn hai hạt được. Hơn nữa, các phương trình này thường có một tính chất được biết là hỗn loạn, do đó, một thay đổi nhỏ về vị trí và vận tốc tại một thời điểm có thể dẫn đến một tính chất hoàn toàn khác tại các thời điểm tiếp theo. Những người đã xem phim Công viên kỷ Jura (Jurassic Park, hình 4.3) đều biết, một xáo trộn nhỏ ở một nơi này có thể gây ra một thay đổi lớn ở một nơi khác. Một con bướm vỗ cánh ở Tokoy có thể gây ra mưa ở công viên trung tâm ở New York. Điều phiền phức là chuỗi sự kiện đó không có tính lặp lại. Lần sau con bướm vỗ cánh, một loạt các sự kiện khác sẽ khác đi và các sự kiện này sẽ ảnh hưởng đến thời tiết. Đó là lý do tại sao các dự báo thời tiết rất không đáng tin cậy.

(Hình 4.3)
Do vậy, mặc dù về nguyên lý thì các định luật của điện động lực học lượng tử sẽ cho phép chúng ta tính toán được tất cả mọi thứ trong hóa học và sinh học, nhưng chúng ta vẫn không có nhiều thành công trong việc đoán trước được hành vi con người từ các phương trình toán học. Tuy nhiên, mặc dù gặp phải những khó khăn trên thực tiễn như thế, nhưng về nguyên tắc, phần lớn các nhà khoa học vẫn được an ủi với ý tưởng cho rằng tương lai vẫn có thể dự báo được.
Thoạt nhìn thì quyết định luận khoa học có vẻ như bị nguyên lý bất định đe dọa. Nguyên lý bất định nói rằng chúng ta không thể đo chính xác vị trí và vận tốc của một hạt tại một thời điểm. Chúng ta đo ví trí càng chính xác bao nhiêu thì chúng ta xác định vận tốc càng kém chính xác bấy nhiêu, và ngược lại. Lối giải thích về quyết định luận khoa học của Laplace cho rằng nếu chúng ta biết vị trí và vận tốc của các hạt tại một thời điểm thì chúng ta có thể xác định được vị trí và vận tốc của chúng tại bất kỳ thời điểm nào trong quá khứ và tương lai. Nhưng làm thế nào mà chúng ta có thể làm được điều đó nếu như ngay từ đầu nguyên lý bất định đã không cho chúng ta biết được vị trí và vận tốc tại một thời điểm? Dù máy tính của chúng ta tốt thế nào đi chăng nữa, nếu chúng 2ta cung cấp dữ liệu đầu vào sai thì chúng ta sẽ nhận được các dự đoán sai lầm.

Tuy vậy, quyết định luận được khôi phục dưới một dạng khác trong một lý thuyết mới được gọi là cơ học lượng tử, tương thích với nguyên lý bất định. Trong cơ học lượng tử, nói một cách gần đúng, ta có thể dự đoán một cách chính xác một nửa những điều mà ta mong muốn thực hiện trên quan điểm Laplace cổ điển. Trong cơ học lượng tử, một hạt không có vị trí hoặc vận tốc xác định nhưng trạng thái của hạt có thể được biểu diễn bằng một cái gọi là hàm sóng (hình 4.4).
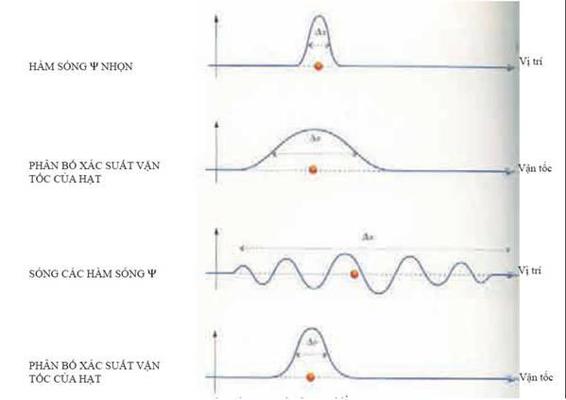
(Hình 4.4)
Hàm sóng xác định xác suất mà hạt sẽ có các vị trí và vận tốc khác nhau theo cách mà chúng phải tuân theo nguyên lý bất định.
Tại mỗi vị trí trong không gian, một hàm sóng là một con số cho biết xác xuất mà hạt có thể được tìm thấy tại vị trí đó. Tốc độ thay đổi của hàm sóng từ điểm này đến điểm khác cho biết khả năng để hạt có các vận tốc khác nhau. Một số hàm sóng có một đỉnh rất nhọn tại một điểm cụ thể trong không gian. Trong trường hợp này, độ bất định về vị trí của hạt là rất nhỏ. Trên giản đồ ta cũng có thể thấy trong những trường hợp đó, hàm sóng thay đổi rất nhanh gần đỉnh của sóng, hàm sóng tăng nhanh ở một sườn và giảm nhanh ở phía sườn kia. Điều này có nghĩa là phân bố xác suất của vận tốc được trải trên một vùng giá trị rất lớn. Hay nói một cách khác, độ bất định về vận tốc rất lớn. Mặt khác, chúng ta hãy xem các hàm sóng thoai thoải thì độ bất định về vị trí lớn nhưng độ bất định về vận tốc lại nhỏ. Vậy nên, việc mô tả các hạt bằng hàm sóng không cho ta vị trí và vận tốc chính xác. Giờ đây ta thấy rằng hàm sóng là tất cả những gì mà ta có thể xác định. Thậm chí chúng ta cũng không thể cho rằng Chúa biết vị trí và vận tốc của các hạt nhưng giấu không cho chúng ta biết. Các lý thuyết “biến số ẩn” (hidden variable) như thế không phù hợp với các quan sát thực nghiệm. Hơn thế nữa, Chúa bị giới hạn bởi nguyên lý bất định và không thể biết vị trí và vận tốc của hạt; Chúa chỉ có thể biết hàm sóng của hạt mà thôi.
Tốc độ thay đổi của hàm sóng theo thời gian được cho bởi một phương trình gọi là phương trình Schrodinger (hình 4.5). Nếu ta biết hàm sóng tại một thời điểm thì chúng ta có thể dùng phương trình Schrodinger để tính hàm sóng tại bất kỳ thời điểm nào khác trong quá khứ và tương lai. Vậy nên, quyết định luận khoa học vẫn đúng trong lý thuyết lượng tử nhưng với một mức độ thấp hơn. Thay cho khả năng đoán trước được cả vị trí và vận tốc, chúng ta chỉ có thể biết được hàm sóng. Hàm sóng chỉ cho biết chính xác vị trí hoặc vận tốc chứ không thể biết được cả hai. Do đó, trong cơ học lượng tử, khả năng tiên đoán chính xác chỉ bằng một nửa khả năng tiên đoán trong thế giới quanLaplace cổ điển. Với ý nghĩa giới hạn này, ta có thể nói quyết định luận khoa học vẫn đúng.
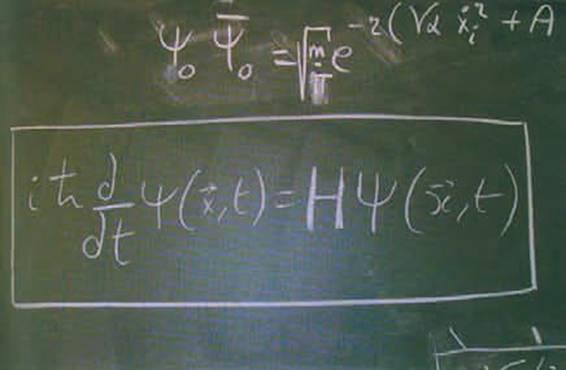
(Hình 4.5)
PHƯƠNG TRÌNH SCHRODINGER
Sự phụ thuộc của hàm sóng Ψ theo thời gian được xác định bởitoán tử H liên quan đến nănglượng của hệ đang xét.
Tuy nhiên, việc dùng phương trình Schrodinger tính hàm sóng theo thời gian (tức là dự đoán những điều sẽ xảy ra trong tương lai) hiển nhiên thừa nhận rằng thời gian trôi đi một cách trơn tru mãi mãi tại khắp các điểm trong không gian. Điều này rõ ràng là đúng trong vật lýNewton. Thời gian được cho là tuyệt đối, tức là mỗi sự kiện trong lịch sử của vũ trụ được đánh dấu bởi một con số được gọi là thời gian và chuỗi con số đó trôi một cách trơn tru từ vô hạn trong quá khứ đến vô hạn trong tương lai. Đó có thể nói là cảm nhận chung về thời gian và là cách nhìn mà phần đông mọi người thậm chí là phần đông các nhà vật lý tâm niệm. Tuy nhiên vào năm 1905, như chúng ta đã thấy, thuyết tương đối hẹp đã vứt bỏ khái niệm thời gian tuyệt đối, trong đó, thời gian tự nó không còn là một đại lượng độc lập của một thể liên tục bốn chiều được gọi là không thời gian. Trong thuyết tương đối hẹp, các nhà quan sát khác nhau chuyển động với các vận tốc khác nhau trong không thời gian theo các hướng khác nhau. Mỗi nhà quan sát có phép đo thời gian riêng của anh ta hoặc cô ta dọc theo hướng mà anh hoặc cô ta đang chuyển động. Và các nhà quan sát khác nhau sẽ đo được các khoảng thời gian khác nhau giữa các sự kiện (hình 4.6).

(Hình 4.6)
Trong không thời gian phẳng của thuyết tương đối hẹp, những người quan sát chuyển động với các tốc độ khác nhau sẽ có các phép đo thời gian khác nhau, nhưng chúng ta có thể dùng phương trình Schrodinger trong bất kỳ thời gian nào để đoán được hàm sóng trong tương lai.
Do đó, trong thuyết tương đối hẹp, không có thời gian tuyệt đối để chúng ta có thể đánh dấu các sự kiện. Tuy nhiên không thời gian trong thuyết tương đối hẹp lại phẳng. Điều này có nghĩa là, trong thuyết tương đối hẹp, thời gian được đo bởi bất kỳ nhà quan sát chuyển động tự do sẽ tăng một cách trơn tru trong không thời gian từ âm vô cùng của quá khứ vô cùng đến dương vô cùng của tương lai vô cùng. Chúng ta có thể dùng bất kỳ phép đo thời gian nào trong phương trình Schrodinger để tính sự phụ thuộc của hàm sóng vào thời gian. Vậy nên, trong thuyết tương đối hẹp, chúng ta vẫn có một kiểu quyết định luận lượng tử.
Trong thuyết tương đối rộng thì tình huống lại khác đi vì không thời gian không còn phẳng mà bị bẻ cong bởi vật chất và năng lượng trong đó. Trong hệ mặt trời của chúng ta, ít nhất là trên nấc thang vĩ mô, độ cong của không thời gian nhỏ đến nỗi nó không ảnh hưởng đến quan niệm chung của chúng ta về thời gian. Trong trường hợp đó, chúng ta vẫn có thể dùng thời gian trong phương trình Schrodinger để biết sự phụ thuộc của hàm sóng vào thời gian. Tuy nhiên, một khi chúng ta cho phép không thời gian có thể bị cong thì khả năng, trong đó không thời gian có một cấu trúc không cho phép thời gian tăng một cách trơn tru đối với mỗi nhà quan sát như chúng ta trông đợi, có thể xảy ra. Ví dụ, không thời gian giống như một hình trụ thẳng đứng (hình 4.7).
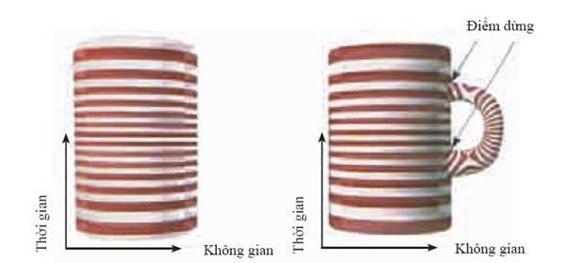
(Hình 4.7)
THỜI GIAN DỪNG
Một phép đo thời gian có thể nhất thiết phải có một điểm dừng mà tại đó quai cầm của chiếc cốc tiếp xúc với phần trụ chính: tại các điểm đó, thời gian sẽ dừng. Tại các điểm như thế, thời gian không tăng theo bất kỳ hướng nào. Do đó, ta có thể dùng phương trình Schrodinger để tiên đoán hàm sóng trong tương lai.
Chiều cao của hình trụ có thể là phép đo thời gian, thời gian tăng đối với mỗi người quan sát và chạy từ âm vô cùng đến dương vô cùng. Tuy nhiên, hãy tưởng tượng rằng, thay cho hình trụ đó là một hình trụ với một cái quai (hoặc là một “hố giun” (wormhole)) tách rời khỏi hình trụ sau đó lại nhập lại. Do đó, bất kỳ phép đo thời gian nào đều có các điểm dừng tại nơi mà cái quai nhập vào hình trụ chính: các điểm mà tại đó thời gian dừng lại. Tại các điểm này thời gian không tăng đối với bất kỳ người quan sát nào. Trong một không thời gian như vậy chúng ta không thể dùng phương trình Schrodinger để biết được sự phụ thuộc của hàm sóng vào thời gian. Hãy cẩn thận với các hố giun: bạn không bao giờ biết được cái gì sẽ chui ra từ đó.
Các hố đen là nguyên nhân để chúng ta nghĩ thời gian không tăng đối với các nhà quan sát. Thảo luận đầu tiên về hố đen xuất hiện vào năm 1783. Một cựu giáo sư của đại học Cambridge, John Michell đã trình bày luận cứ sau đây: nếu ai đó bắn một hạt, như là một viên đạn đại bác chẳng hạn, thẳng lên trời thì chuyển động lên trên sẽ bị chậm lại do lực hấp dẫn và cuối cùng là hạt sẽ dừng chuyển động lên trên và sẽ rơi trở lại (hình 4.8). Tuy vậy nếu vận tốc bắn ban đầu lớn hơn một vận tốc tới hạn được gọi là vận tốc thoát thì lực hấp dẫn sẽ không đủ mạnh để dừng hạt đó lại và hạt đó sẽ bay đi. Trên trái đất, vận tốc thoát vào khoảng 12 km/giây; trên mặt trời thì giá trị đó vào khoảng 618 km/giây.


(Hình 4.8)
Cả hai vận tốc thoát đó đều lớn hơn nhiều vận tốc của các viên đạn đại bác nhưng lại nhỏ hơn vận tốc ánh sáng (vào khoảng 300.000 km/giây). Vậy nên ánh sáng có thể thoát khỏi trái đất và mặt trời một cách không mấy khó khăn. Nhưng Michell lại lý luận rằng có thể có các ngôi sao lớn hơn nhiều lần mặt trời và có vận tốc thoát lớn hơn vận tốc ánh sáng (hình 4.9). Chúng ta không thể nhìn thấy các ngôi sao đó vì bất kỳ tia sáng nào được phóng đi sẽ bị lực hấp dẫn của ngôi sao kéo trở lại.

(Hình 4.9)
Ý tưởng về các ngôi sao tối của Michell dựa trên nền vật lý củaNewton, trong đó thời gian là tuyệt đối và thời gian không đếm xỉa đến những sự kiện xảy ra. Vậy nên, trong bức tranh vật lý cổ điển củaNewton, các ngôi sao đen không ảnh hưởng đến khả năng tiên đoán tương lai của chúng ta. Nhưng trong thuyết tương đối rộng, trong các vật thể khổng lồ làm cong không thời gian thì tình huống lại khác hẳn.
Năm 1916, ngay sau khi thuyết tương đối rộng được đưa ra lần đầu tiên, Karl Schwarzschild (ông đã mất ngay sau khi mắc bệnh ở mặt trận với Nga trong đại chiến thế giới lần thứ nhất) đã tìm thấy một nghiệm của các phương trình trường của thuyết tương đối rộng biểu diễn cho một hố đen. Trong rất nhiều năm, người ta không hiểu hoặc không nhận ra tầm quan trọng của những điều mà Schwarzschild đã tìm ra. Bản thân Einstein cũng không bao giờ tin vào các hố đen và quan điểm của ông cũng được phần lớn các nhà khoa học có uy tín về thuyết tương đối chia sẻ. Tôi còn nhớ chuyến đi Paris để trình bày một báo cáo về phát hiện của tôi cho rằng thuyết lượng tử ngụ ý các hố đen không hoàn toàn đen. Báo cáo của tôi khá tẻ nhạt vì vào lúc đó gần như không có ai ở Paris tin vào các hố đen. Người Pháp còn cảm thấy rằng cái tên trou noir mà họ dịch ra tiếng Pháp có nghĩa hơi tục tĩu và nên thay bằng cái tên astre occlu tức là “ngôi sao ẩn” (hidden star). Tuy vậy, dù là ngôi sao ẩn hoặc bất kỳ tên nào khác cũng không nhận được sự nhìn nhận của công chúng bằng cái tên hố đen. Đây là tên do Archibald Wheeler đưa ra. Ông là một nhà vật lý Mỹ, người đã gây nhiều cảm hứng cho các công trình trong lĩnh vực này.
JOHN WHEELER
John Chibald Wheeler sinh năm 1911 tại Jacksonville, Florida, Hoa Kỳ. Ông lấy bằng tiến sỹ về tán xạ của ánh sáng lên nguyên tử Helium ở đại học John Hopkins năm 1933. Năm 1938 ông làm việc cùng nhà vật lý Đan Mạch Niels Bohr để phát triển lý thuyết phân hạch. Sau đó một thời gian, ông làm việc cùng với sinh viên của ông là Richard Feynman, tập trung nghiên cứu nhiệt động học; nhưng ngay sau khi Hoa Kỳ tham gia đại chiến thế giới 2, cả hai đều đóng góp vào sự án Mahattan.
Vào những năm đầu thập kỷ 50, lấy cảm hứng từ công trình về sự suy sụp hấp dẫn của những ngôi sao nặng của Robert Oppenheimer vào năm 1939, Wheeler chuyển sang thuyết tương đối rộng của Einstein. Vào thời gian đó, phần lớn các nhà vật lý đều nghiên cứu vật lý hạt nhân và thuyết tương đối rộng không thực sự được coi là phù hợp với thế giới vật lý. Nhưng gần như một mình Wheeler đơn thương độc mã làm thay đổi lĩnh vực nghiên cứu thông qua các công trình của ông và thông qua việc giảng dạy khóa học đầu tiên về thuyết tương đối ở đại học Princeton.
Rất lâu sau, vào năm 1969, ông đưa ra khái niệm “hố đen”, mà lúc bấy giờ chỉ có một số ít người tin rằng nó tồn tại, để chỉ trạng thái suy sụp của vật chất. Và từ công trình của Werner Israel, ông dự đoán rằng hố đen không có tóc, ám chỉ trạng thái suy sụp cả bất kỳ ngôi sao nặng không quay nào cũng có thể được mô tả bằng nghiệm Schswarzschild.
Sự phát hiện ra các quasar vào năm 1963 đã gây ra một cuộc bùng phát các nghiên cứu lý thuyết về hố đen và các nỗ lực quan sát để nhìn thấy chúng (hình 4.10). Đây là bức tranh được ghép lại. Hãy xem xét những điều chúng ta tin về lịch sử của một ngôi sao có khối lượng lớn gấp hai mươi lần khối lượng mặt trời. Các ngôi sao như vậy được hình thành từ các đám mây khí như là các ngôi sao trong tinh vân Thiên Lang (Orion, hình 4.11). Khi các đám mây khí co lại dưới lực hấp dẫn của chính bản thân chúng, các khí này sẽ nung nóng và thậm chí trở nên đủ nóng để khởi động phản ứng nhiệt hạch biến hydro thành helium. Nhiệt tạo bởi quá trình này gây nên một áp suất giúp ngôi sao chống trọi lại lực hấp dẫn của nó và làm cho ngôi sao không bị co thêm nữa. Ngôi sao sẽ ở trạng thái này trong một thời gian dài, đốt cháy hydro và bức xạ ánh sáng vào không gian.

(Hình 4.10)
Quasar 3C273, nguồn phát sóng vô tuyến giả sao đầu tiên được phát hiện, phát ra một năng lượng rất lớn trong một vùng nhỏ. Cơ chế duy nhất để giải thích hiện tượng độ sáng cao như thế là vật chất đang rơi vào hố đen.

(Hình 4.11)
Các ngôi sao được hình thành từ các đám bụi khí giống như tinh vân Thiên Lang.
Trường hấp dẫn của ngôi sao sẽ ảnh hưởng đến đường truyền của chùm sáng phát ra từ ngôi sao đó. Ta có thể vẽ một giản đồ với thời gian là trục thẳng đứng, khoảng cách từ tâm của ngôi sao là trục nằm ngang (hình 4.12). Trong giản đồ này, bề mặt của ngôi sao được biểu diễn bằng hai đường thẳng đứng nằm hai bên của tâm sao. Ta có thể đo thời gian bằng giây và khoảng cách bằng “giây ánh sáng” - khoảng cách mà ánh sáng đi được trong một giây. Khi ta dùng các đơn vị này thì tốc độ của ánh sáng là 1; tức là, tốc độ của ánh sáng là một giây ánh sáng trên giây. Giản đồ ngụ rằng, ở phía xa ngôi sao, xa trường hấp dẫn của nó thì đường truyền của tia sáng trên giản đồ là một đường thẳng tạo với trục thẳng đứng một góc 45 độ. Tuy nhiên, gần ngôi sao thì độ cong của không thời gian do khối lượng của ngôi sao gây ra sẽ làm thay đổi đường truyền của các tia sáng và làm cho chúng tạo với phương thẳng đứng một góc hẹp hơn.
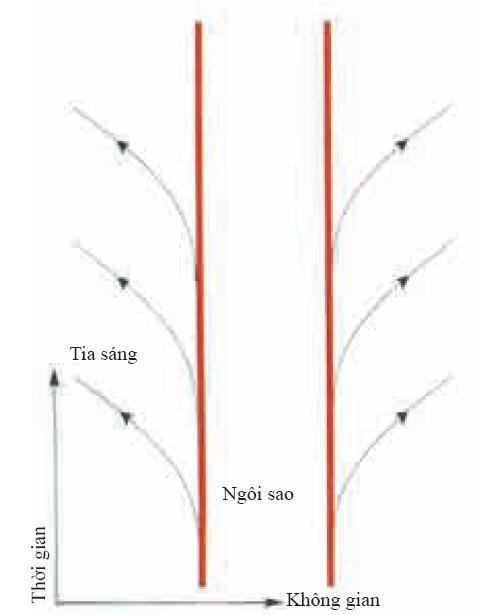
(Hình 4.12)
Không thời gian xung quanh một ngôi sao không bị suy sập. Ánh sáng có thể thoát ra từ bề mặt ngôi sao (đường thẳng đứng màu đỏ). Ở xa ngôi sao, ánh sáng tạo với phương thẳng đứng một góc 45 độ, nhưng ở gần ngôi sao, khối lượng của ngôi sao làm cong không thời gian làm cho các tia sáng làm một góc nhỏ hơn với phương thẳng đứng.
Các ngôi sao nặng sẽ đốt cháy hydro thành helium nhanh hơn mặt trời rất nhiều. Điều này có nghĩa là chúng sẽ cạn kiệt hydro chỉ trong một thời gian ngắn khoảng vài trăm triệu năm. Sau đó, các ngôi sao này sẽ đối mặt với một cuộc khủng hoảng. Chúng có thể đốt helium thành các nguyên tố nặng hơn như là carbon và oxygen, nhưng các phản ứng hạt nhân này không giải thoát nhiều năng lượng, do đó các ngôi sao sẽ mất nhiệt và mất đi áp suất nhiệt giúp ngôi sao chống lại lực hấp dẫn. Do đó các ngôi sao trở nên nhỏ hơn. Nếu khối lượng của chúng lớn hơn hai lần khối lượng mặt trời thì áp suất sẽ không bao giờ đủ để ngăn chặn quá trình co lại. Chúng sẽ suy sụp thành một điểm với mật độ vô hạn tạo nên cái gọi là điểm kỳ dị (hình 4.13). Trong giản đồ thời gian theo khoảng cách từ tâm ngôi sao, khi một ngôi sao co lại thì đường truyền của các tia sáng từ bề mặt ngôi sao sẽ tạo với đường thẳng đứng những góc nhỏ hơn và nhỏ hơn. Khi ngôi sao đạt đến một bán kính tới hạn xác định thì các đường truyền của tia sáng sẽ là đường thẳng đứng trên giản đồ, tức là ánh sáng sẽ đi trên một khoảng các cố định với tâm ngôi sao mà không bao giờ có thể thoát đi được. Đường truyền tới hạn của tia sáng sẽ lướt trên một bề mặt được gọi là chân trời sự kiện (event horizon) phân cách vùng không thời gian mà ánh sáng có thể thoát khỏi ngôi sao và vùng không thời gian mà ánh sáng không thể thoát được. Bất kỳ một tia sáng nào được ngôi sao phát đi sau khi đi qua chân trời sự kiện sẽ bị bẻ cong trở lại bởi độ cong của không thời gian. Ngôi sao sẽ trở thành một trong những ngôi sao đen của Michell, hoặc như ngày nay chúng ta nói, một hố đen.
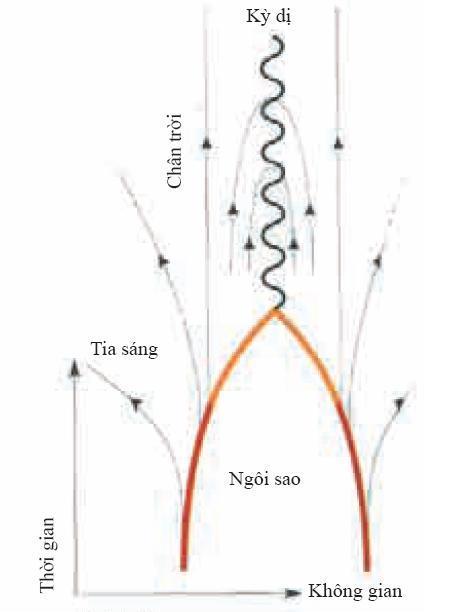
(Hình 4.13)
Nếu một ngôi sao suy sập (đường màu đỏ cắt nhau tại một điểm) không thời gian bị bẻ cong đến nỗi ánh sáng gần bề mặt bị hướng vào trong. Một hố đen được hình thành, một vùng không thời gian mà ánh sáng từ đó không thể thoát ra được.
Chân trời là vùng biên giới của một hố đen được hình thành bởi các tia sáng chỉ chớm không thoát khỏi hố đen và giữ một khoảng cách không đổi với tâm của hố đen.
Làm thế nào để có thể ghi nhận một hố đen nếu không một tia sáng nào có thể thoát khỏi nó? Câu trả lời là hố đen vẫn tạo ra một lực hút hấp dẫn không đổi lên các vật thể lân cận khi ngôi sao bị suy sụp. Nếu mặt trời là một hố đen hoặc trở thành một hố đen mà không mất đi khối lượng của nó thì thì các hành tinh vẫn quay như chúng đang quay hiện nay.
Có một cách để tìm kiếm các hố đen đó là tìm kiếm vật chất quay xung quanh một vật thể khổng lồ, đặc và không nhìn thấy. Người ta đã quan sát rất nhiều các hệ như thế. Có lẽ ấn tượng nhất là các hố đen khổng lồ xuất hiện ở tâm của các thiên hà và các quasar (hình 4.15).
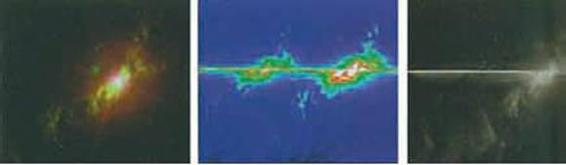
(Hình 4.15)
MỘT HỐ ĐEN Ở TÂM THIÊN HÀ
Trái: Phát hiện thiên hà NGC 4151 từ ống kính thiên hà trường rộng.
Giữa: Đường nằm ngang bức hình là ánh sáng phát ra từ một hố đen ở tâm thiên hà 4151.
Phải: Hình này cho thấy tốc độ phát ra oxygen. Tất cả các bằng chứng đều cho thấy rằng NGC 4151 có chứa một hố đen có khối lượng bằng một trăm triệu lần khối lượng mặt trời.
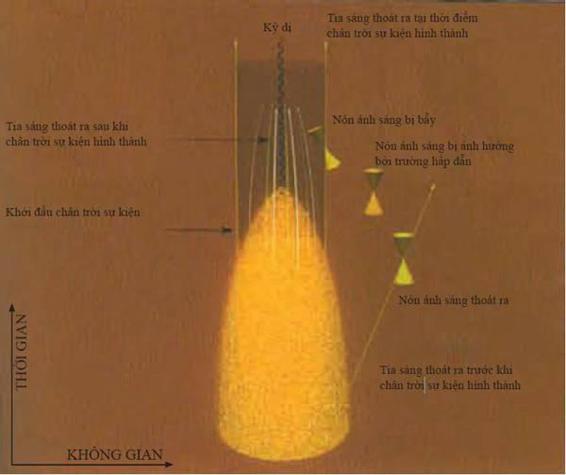
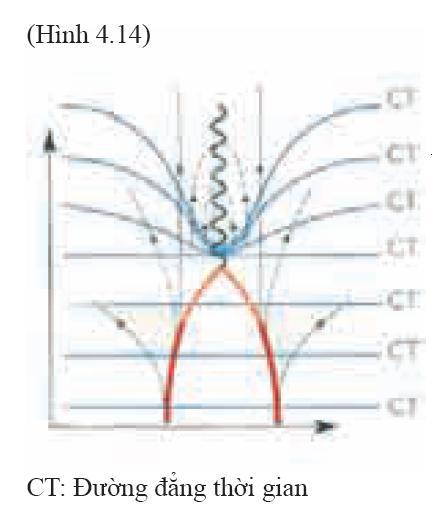
Các tính chất của hố đen đã được thảo luận cho đến nay không gây nên vấn đề lớn nào cho quyết định luận. Thời gian sẽ kết thúc đối với nhà du hành vũ trụ rơi vào hố đen và chạm vào điểm kỳ dị. Tuy nhiên, trong thuyết tương đối, người ta hoàn toàn tự do khi đo thời gian với các tốc độ khác nhau và tại các địa điểm khác nhau. Do đó, người ta có thể tăng tốc đồng hồ của nhà du hành vũ trụ khi anh ta hoặc cô ta tiến đến gần điểm kỳ dị, vậy nên, người ta vẫn ghi nhận được khoảng thời gian vô tận. Trên giản đồ thời gian - khoảng cách (hình 4.14), các mặt phẳng mà tại đó thời gian là hằng số sẽ rất dày đặc tại trung tâm - bên dưới điểm mà tại đó kỳ dị xuất hiện. Nhưng các mặt phẳng đó lại phù hợp với phép đo thời gian thông thường tại vùng không thời gian gần phẳng cách xa hố đen.

Hình minh họa một nhà du hành hạ cách xuống một ngôi sao đang suy sập vào hồi 11 giờ 59 phút 57 giây và chạm vào ngôi sao đang co lại tới bán kính tới hạn mà tại đó hấp dẫn mạnh đến nỗi không một tín hiệu nào có thể thoát ra được. Nhà du hành gửi tín hiệu từ đồng hồ của anh ta về phi thuyền đang quay cách quanh ngôi sao một khoảng cách tương đối lớn.
Một ai đó đang nhìn ngôi sao từ phía xa sẽ không bao giờ nhìn thấy nó đi qua đường chân trời vào hố đen. Thay vào đó, ngôi sao có vẻ như lượn lờ bên ngoài kích thước tới hạn và đồng hồ trên bề mặt ngôi sao sẽ chậm dần rồi tắt hẳn.
Ta có thể dùng thời gian trong vùng không thời gian gần phẳng cho phương trình Schrodinger và tình hàm sóng tại các thời điểm sau đó nếu ta biết thời gian trước đó. Do đó, ta vẫn có quyết định luận. Tuy vậy, cũng đáng lưu ý rằng, tại các thời điểm sau, một phần của hàm sóng lại ở bên trong hố đen - nơi mà không ai bên ngoài có thể quan sát thấy hàm sóng đó. Vì thế, một người quan sát - người đủ nhạy cảm để không bị rơi vào hố đen, không thể chạy ngược phương trình Schrodinger để tính hàm sóng tại các thời điểm trước đó. Để làm điều đó, anh ta hoặc cô ta cần biết phần của hàm sóng nằm bên trong hố đen. Phần hàm sóng này có chứa các thông tin về những cái rơi vào hố đen. Rất có khả năng đó là một lượng lớn các thông tin vì hố đen với khối lượng và tốc độ quay đã cho có thể được tạo thành từ rất nhiều tập hợp các hạt khác nhau; hố đen không phụ thuộc vào bản chất vật thể suy sụp để tạo nên nó. John Wheeler gọi kết quả này là “hố đen không có tóc”. Đối với người Pháp, điều này khẳng định các mối nghi ngờ của họ.

Hố đen không có tóc
Khó khăn cho quyết định luận xuất hiện khi tôi thấy rằng các hố đen không phải là hoàn toàn đen. Như là ta đã thấy trong chương 2, thuyết lượng tử ngụ ý rằng các trường có thể không hoàn toàn bằng không ngay cả trong cái mà ta gọi là chân không. Nếu chúng bằng không thì chúng sẽ có cả vị trí tại điểm không và tốc độ thay đổi hay còn gọi là vận tốc cũng bằng không. Điều ngày vi phạm nguyên lý bất định nói rằng người ta không thể xác định chính xác vận tốc và vị trí. Thay vào đó, tất cả các trường cần phải có một cái gọi là thăng giáng chân không nhất định (tương tự như là con quay trong chương 2 phải có thăng giáng điểm không). Thăng giáng chân không có thể được giải thích theo một vài cách có vẻ khác nhau nhưng thực tế là chúng tương đương với nhau về mặt toán học. Trên quan điểm thực chứng, ta không bị bó buộc khi sử dụng bất kỳ mô hình nào hiệu quả nhất cho bài toán đặt ra. Trong trường hợp này, sẽ rất có ích khi coi thăng giáng chân không như các cặp hạt ảo xuất hiện cùng nhau tại một điểm trong không thời gian, chuyển động ra xa nhau rồi quay trở lại với nhau và hủy nhau lẫn nhau. “Ảo” có nghĩa là các hạt này không thể được quan sát một cách trực tiếp, nhưng ta có thể đo được các hiệu ứng gián tiếp, và các phép đo này phù hợp với các tiên đoán lý thuyết với một độ chính xác đáng kể (hình 4.16).

(Hình 4.16)
Trong không gian trống rỗng, các cặp hạt xuất hiện trong khoảnh khắc rồi hủy lẫn nhau.

(Hình 4.17)
Các hạt ảo xuất hiện và hủy lẫn nhau ở gần chân trời sự kiện của hố đen.
Một hạt bị rơi vào hố đen trong khi hạt kia thoát ra ngoài. Từ bên ngoài chân trời sự kiện dường như hố đen đang bức xạ các hạt ra không gian.
Nếu hố đen hiện diện thì một thành phần của cặp hạt có thể bị rơi vào hố đen để lại thành phần kia tự do thoát vào vô tận (hình 4.17). Đối với một người ở phía xa hố đen thì hạt thoát ra kia dường như được phát xạ từ hố đen. Ta trông đợi phổ của hố đen chính là phổ của một vật nóng với nhiệt độ tỷ lệ với trường hấp dẫn tại chân trời sự kiện - biên giới của hố đen. Nói cách khác, nhiệt độ của hố đen phụ thuộc vào kích thước của nó.
NHIỆT ĐỘ CỦA HỐ ĐEN
Hố đen phát xạ giống như một vật nóng có nhiệt độ (T) và chỉ phụ thuộc vào khối lượng của nó. Nói chính xác hơn là nhiệt độ đó cho bởi công thức sau:
T = hc3/8πkGM
Trong công thức này (c) là vận tốc ánh sáng, (h) là hằng số Plank, (G) là hằng số hấp dẫn Newton, (k) là hằng số Boltzman.
Cuối cùng là (M) là khối lượng của hố đen, do đó, hố đen càng nhỏ thì nhiệt độ càng cao. Công thức này cho chúng ta thấy rằng, nhiệt độ của một hố đen có khối lượng bằng vài lần khối lượng mặt trời có nhiệt độ chỉ khoảng một phần triệu độ trên không độ tuyệt đối.
Một hố đen có khối lượng gấp vài lần khối lượng mặt trời sẽ có nhiệt độ khoảng một phần triệu độ trên không độ tuyệt đối, và một hố đen lớn hơn lại có nhiệt độ thấp hơn. Do vậy, bất kỳ bức xạ lượng tử nào từ các hố đen như thế sẽ bị chìm hoàn toàn trong bức xạ 2,7 độ còn sót lại từ vụ nổ lớn - bức xạ phông vũ trụ mà ta đã thảo luận trong chương 2. Ta có thể ghi được bức xạ từ các hố đen nhỏ hơn và nóng hơn, nhưng dường như không có nhiều các hố đen như thế. Thật đáng tiếc! Nếu người ta phát hiện ra một hố đen thì tôi sẽ được giải Nobel. Tuy nhiên chúng ta vẫn có những bằng chứng khả quan gián tiếp về bức xạ này, bằng chứng này đến từ vũ trụ sơ khai. Như đã mô tả trong chương 3, người ta cho rằng vào những giai đoạn rất sớm trong lịch sử, vũ trụ trải qua một thời kỳ lạm phát, khi đó vũ trụ giãn nở với một tốc độ chưa từng có. Quá trình giãn nở trong thời kỳ này nhanh đến nỗi một số vật thể ở quá xa chúng ta và ánh sáng của chúng không bao giờ đến được với chúng ta. Vũ trụ giản nở quá nhiều và quá nhanh trong khi ánh sáng từ chúng truyền vẫn hướng về chúng ta. Do đó sẽ có một chân trời trong vũ trụ giống như chân trời của hố đen, phân cách vùng mà ánh sáng từ đó có thể đến với chúng ta và vùng mà ánh sáng không thể đến với ta được (hình 4.18).
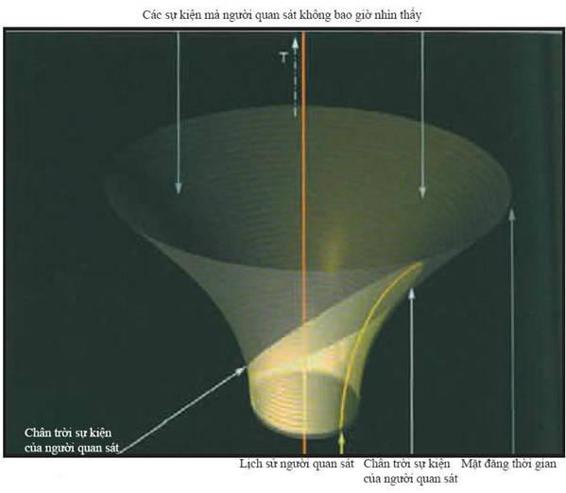
(Hình 4.18)
Nghiệm “de Sitter” của các phương trình trường của thuyết tương đối biểu diễn một vũ trụ giãn nở theo kiểu lạm phát. Trên giản đồ, thời gian hướng lên trên và kích thước của vũ trụ theo phương nằm ngang. Khoảng cách về không gian tăng nhanh đến mức ánh sáng từ các thiên hà xa xôi không bao giờ có thể đến với chúng ta, và do đó, có một chân trời sự kiện giống chân trời sự kiện của hố đen, một biên giới ngăn cách những vùng vũ trụ ta không thể quan sát được.
Các lập luận tương tự cho thất rằng có một bức xạ nhiệt từ chân trời này giống như bức xạ nhiệt từ chân trời của hố đen. Từ bức xạ nhiệt, chúng ta muốn biết phổ đặc trưng của các thăng giáng mật độ. Ở đây, các thăng giáng mật độ này cũng giãn nở cùng vũ trụ. Khi kích thước của chúng trở lên lớn hơn kích thước của chân trời sự kiện thì chúng sẽ bị đóng băng, cho nên ngày nay ta có thể thấy chúng như là những thăng giáng nhỏ trong nhiệt độ của bức xạ phông vũ trụ còn lại từ thời kỳ sơ khai của vũ trụ. Các thăng giáng quan sát phù hợp với các tiên đoán về thăng giáng nhiệt với độ chính xác cao.
Thậm chí nếu bằng chứng thực nghiệm về bức xạ của hố đen không trực tiếp cho lắm thì tất cả những ai nghiên cứu vấn đề này đều đồng ý rằng bằng chứng đó cần phải phù hợp với các lý thuyết khác mà đã được kiểm chứng bằng các quan sát. Điều này có ý nghĩa rất quan trọng đối với quyết định luận. Bức xạ từ hố đen sẽ mang năng lượng đi, điều này có nghĩa là hố đen sẽ mất năng lượng và trở nên nhỏ đi. Và sự nhỏ đi này, đến lượt nó, có nghĩa là nhiệt độ của hố đen sẽ tăng và tốc độ bức xạ cũng sẽ tăng. Cuối cùng thì hố đen sẽ giảm đến khối lượng bằng không. Lúc đó thì ta không biết làm thế nào để có thể tính được việc gì sẽ xảy ra, nhưng kết quả duy nhất hợp lý và đương nhiên là hố đen dường như biến mất hoàn toàn. Thế thì cái gì sẽ xảy ra sau đó đối với phần hàm sóng nằm trong hố đen và thông tin về những cái đã rơi vào hố đen mà phần hàm sóng đó có? Dự đoán đầu tiên có thể là phần hàm sóng này, và các thông tin mà nó mang, sẽ thoát ra khi hố đen cuối cùng thì cũng biến mất. Tuy nhiên, thông tin không được truyền đi một cách miễn phí, người ta nhận ra điều đó khi nhận được hóa đơn điện thoại!
Thông tin cần năng lượng mang nó đi và lại có rất ít năng lượng còn sót lại ở trạng thái cuối cùng của hố đen. Cách duy nhất có vẻ hợp lý để thông tin bên trong có thể đi được ra ngoài là nó sẽ thoát ra liên tục với bức xạ chứ không đợi đến trạng thái cuối cùng này. Tuy nhiên, theo bức tranh về một hạt của cặp hạt ảo bị rơi vào hố đen và hạt kia thoát ra ngoài, ta không trông đợi hạt thoát ra ngoài có liên hệ với hạt bị rơi vào hố đen hoặc mang đi thông tin về hạt bị rơi vào hố đen. Do vậy câu trả lời duy nhất dường như là thông tin của phần hàm sóng bên trong hố đen bị mất (hình 4.19).

(Hình 4.19)
Bức xạ nhiệt từ chân trời sự kiện của hố đen mang năng lượng dương đi làm giảm khối lượng của nó. Vì mất đi khối lượng, nhiệt độ của hố đen tăng lên và tốc độ bức xạ cũng gia tăng làm cho khối lượng của nó giảm đi càng nhanh. Chúng ta không biết điều gì xảy ra nếu khối lượng trở lên cực nhỏ, nhưng kết quả hợp lý nhất có thể là hố đen biến mất hoàn toàn.
Sự mất mát thông tin như thế có hàm ý rất quan trọng với quyết định luận. Để bắt đầu, ta hãy lưu ý rằng, thậm chí, nếu bạn biết hàm sóng sau khi hố đen biến mất thì bạn cũng không thể chạy ngược phương trình Schrodinger và tính xem hàm sóng đó như thế nào trước khi hố đen được hình thành. Hàm sóng trước đó phụ thuộc một phần vào hàm sóng bị mất trong hố đen. Chúng ta đã từng nghĩ là chúng ta biết quá khứ một cách chính xác. Tuy nhiên, nếu thông tin bị mất trong hố đen thì suy nghĩ đó không còn đúng nữa. Bất kỳ điều gì cũng có thể xảy ra.
Mặc dù vậy thì nói chung mọi người như là các nhà du hành vũ trụ và những người tư vấn cho họ quan tâm đến việc tiên đoán tương lai hơn là xem xét lại quá khứ. Thoạt nhìn, có vẻ như là việc mất một phần hàm sóng trong hố đen không ngăn cản chúng ta tiên đoán hàm sóng bên ngoài hố đen. Nhưng hóa ra sự mất mát này lại tác động đến tiên đoán như thế, như chúng ta sẽ thấy khi ta xem xét một thí nghiệm về tư duy do Einstein, Boris Podolsky và Nathan Rosen đề xuất vào những năm 1930.
Hãy hình dung một nguyên tử phóng xạ phân rã và phát ra hai hạt đi theo hai hướng ngược nhau với spin cũng ngược nhau. Một người quan sát mà chỉ nhìn vào một hạt thì không thể tiên đoán hạt đó sẽ quay phải hay quay trái. Nếu người quan sát đo được một hạt quay phải thì anh ta hoặc cô ta có thể đoán chắc chắn là hạt kia sẽ quay trái, và ngược lại (hình 4.20). Einstein cho rằng điều này chứng minh thuyết lượng tử thật nực cười: giả sử bây giờ hạt kia ở phía bên kia của thiên hà, người ta vẫn có thể biết ngay tức thì hướng quay của nó. Tuy vậy, phần lớn các nhà khoa học đồng ý rằng chính Einstein lầm lẫn chứ không phải thuyết lượng tử. Thí nghiệm về tư duy Einstein-Podolsky-Rosen không chứng minh rằng người ta có thể gửi thông tin nhanh hơn ánh sáng. Mà đó chính là điều nực cười. Người ta không thể chọn hạt quay phải để quan sát nên người ta không thể đoán trước được hạt ở phía xa người quan sát sẽ quay trái.

(Hình 4.20)
Trong thí nghiệm tư duy Einstein-Podolsky-Rosen, một người quan sát đo spin của một hạt sẽ biết hướng spin của hạt thứ hai.
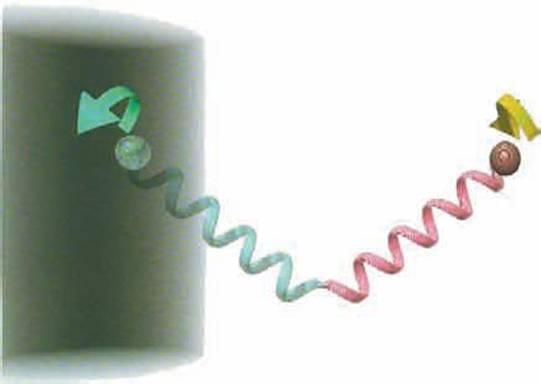
(Hình 4.21)
Một cặp hạt ảo có một hàm sóng tiên đoán cả hai hạt có spin ngược nhau. Nhưng nếu một hạt bị rơi vào hố đen thì ta không thể đoán được chắc chắn spin của hạt còn lại.
Trên thực tế, thí nghiệm về tư duy này chính là những điều xảy ra với bức xạ hố đen. Cặp hạt ảo sẽ có một hàm sóng tiên đoán rằng hai hạt đó sẽ mãi có spin ngược nhau (hình 4.21). Điều mà chúng ta muốn làm đó là đoán spin và hàm sóng của hạt thoát ra. Ta có thể làm được điều này nếu ta có thể quan sát được hạt bị rơi vào hố đen. Nhưng hạt đó ở trong hố đen thì ta không thể đo được spin và hàm sóng của nó. Vậy nên ta không thể tiên đoán spin và hàm sóng của hạt thoát ra. Hạt đó có thể có các spin khác, các hàm sóng khác với các xác suất khác nhau, nhưng nó không có một spin hoặc một hàm sóng duy nhất. Vậy nên, khả năng tiên đoán tương lai của chúng ta dường như bị giới hạn hơn. Ý tưởng cổ điển của Laplace về việc ta có thể tiên đoán cả vị trí và vận tốc của hạt cần phải thay đổi khi nguyên lý bất định cho thấy rằng ta không thể đo chính xác cả vị trí và vận tốc. Tuy nhiên, người ta vẫn có thể đo được hàm sóng và sử dụng phương trình Schrodinger để biết tương lai sẽ như thế nào. Điều này cho phép ta chắc chắn đoán được tổ hợp của vị trí và vận tốc - đó là một nửa của những điều có thể đoán trước theo ý tưởng của Laplace. Chắc chắn là ta có thể tiên đoán các hạt có spin ngược nhau, nhưng nếu một hạt bị rơi vào hố đen thì chúng ta không thể tiên đoán chắc chắn về hạt còn lại. Điều này có nghĩa là người ta không thể tiên đoán chắc chắn bất kỳ phép đo nào bên ngoài hố đen: khả năng tiên đoán chắc chắn của chúng ta bị giảm về không. Do vậy ngành chiêm tinh học có thể tiên đoán tương lai không tồi hơn các định luật khoa học.
Nhiều nhà vật lý không thích sự suy giảm trong quyết định luận và do đó, họ cho rằng thông tin về những thứ bên trong có thể thoát ra ngoài bằng cách nào đó. Trong nhiều năm, người ta hảo vọng tìm thấy cách để cứu lấy thông tin. Nhưng vào năm 1996, Andrew Strominger và Cumrun Vafa đã thực hiện một cải tiến quan trọng. Họ coi một hố đen được tạo nên bởi các thành phần được gọi là các màng-p (p-branne: xem trang 54).

(Hình 4.22)
Các hố đen có thể được coi như là phần giao nhau của các màng-p trong các chiều bổ sung của không thời gian. Thông tin về các trạng thái bên trong hố đen có thể được lưu trữ dưới dạng các sóng trên màng-p.
Nhắc lại là ta có thể hình dung về các màng-p như là các tấm chuyển động trong không gian ba chiều và trong bảy chiều bổ sung mà ta không để ý (hình 4.22). Trong một số trường hợp nhất định, ta có thể chứng minh rằng số các sóng trên các màng-p bằng lượng thông tin mà ta trông đợi hố đen có. Nếu các hạt đập vào màng-p, các hạt đó sẽ tạo ra thêm các sóng trên các màng đó. Tương tự, nếu các sóng đang chuyển động theo các hướng khác nhau trên các màng-p mà gặp nhau tại một điểm nào đó thì chúng có thể tạo nên một đỉnh sóng lớn đến nỗi làm cho một phần của màng-p bị đứt và thoát ra ngoài như một hạt. Vậy nên các màng-p có thể hấp thụ và phát xạ các hạt giống như hố đen (hình 4.23).


(Hình 4.23)
Một hạt bị rơi vào hố đen có thể được coi như một vòng dây kín đập vào màng-p (1). Nó kích thích một sóng trên màng-P (2). Các sóng đó có thể đi với nhau làm cho một phần của màng-p bị đứt ra tạo một vòng dây kín (3). Đấy là một hạt thoát ra khỏi hố đen.

Ta có thể coi các màng-p như là một lý thuyết hiệu dụng; tức là, chúng ta không cần tin rằng thực sự có các màng tí hon chuyển động trong một không thời gian phẳng hay không, thì các hố đen vẫn có thể xử sự như thể chúng được tạo thành từ các màng như vậy. Giống như nước vậy, nước được tạo thành từ hàng tỷ tỷ các phân tử H2O với các tương tác phức tạp. Nhưng mô hình chất lỏng liên tục là mô hình hiệu dụng rất tốt. Mô hình toán học về các hố đen cho rằng chúng được tạo thành từ các màng-p cho các kết quả tương tự với mô hình cặp hạt ảo được mô tả trước đây. Do đó, trên quan điểm thực chứng, đây cũng là một mô hình rất tốt, ít nhất là đối với một số loại hố đen nhất định. Đối với loại hố đen đó, mô hình màng-p tiên đoán một cách chính xác tốc độ phát xạ mà mô hình cặp hạt ảo đưa ra. Tuy nhiên, có một sự khác nhau quan trọng: trong mô hình màng-p, thông tin về những cái rơi vào hố đen được lưu trữ bởi hàm sóng của các sóng trên các màng-p. Các màng-p được coi như là các tấm trong không gian phẳng, và vì lý do đó, thời gian sẽ trôi đi một cách trơn tru, đường truyền của các tia sáng sẽ không bị bẻ cong, và thông tin trong các sóng sẽ không bị mất. Thay vào đó, cuối cùng thì thông tin hiện ra từ hố đen theo các bức xạ từ các màng-p. Vậy nên, theo mô hình màng-p, chúng ta có thể sử dụng phương trình Schrodinger để tính hàm sóng tại các thời điểm sau đó. Không có gì bị mất cả, thời gian sẽ quay đều đặn. Chúng ta sẽ có một quyết định luận hoàn hảo theo nghĩa lượng tử.

Thế thì bức tranh nào trong hai bức tranh trên là đúng? Một phần hàm sóng sẽ bị mất trong hố đen hay tất cả các thông tin sẽ thoát ra như màng-p dự đoán? Đây là một trong những câu hỏi nổi cộm nhất trong vật lý lý thuyết ngày nay. Nhiều người tin rằng công trình gầy đây cho thấy thông tin sẽ không bị mất. Thế giới là an toàn và có thể dự đoán được, sẽ không có gì bất ngờ xảy ra. Nhưng điều đó vẫn chưa rõ ràng. Nếu ta chọn thuyết tương đối rộng của Einstein một cách nghiêm túc thì ta phải thừa nhận xác xuất mà không thời gian tự trói mình như một cái nơ và thông tin bị mất trong những nếp gấp. Khi phi thuyềnEnterprise đi qua một hố giun, vài điều bất ngờ đã xảy ra. Tôi biết điều đó vì chính tôi đã ở trên phi thuyền đó chơi bài với Newton, Einstein và Data. Tôi đã rất ngạc nhiên. Hãy xem cái gì đã xảy ra ở đầu gối của tôi này!

Một cảnh trong phim Star Trek: The Next Generation, 2001



 ePub
ePub A4
A4